直方图
简介
在统计学中,直方图(英语:histogram)是一种对数据分布情况的图形表示,是一种二维统计图表,它的两个坐标分别是统计样本和该样本对应的某个属性的度量,以长条图(bar)的形式具体表现。因为直方图的长度及宽度很适合用来表现数量上的变化,所以较容易解读差异小的数值。
相关概念
- 组数:在统计数据时,我们把数据按照不同的范围分成几个组,分成的组的个数称为组数
- 组距:每一组两个端点的差
- 频数:分组内的�数据元的数量除以组距
频数分布直方图
非标准的直方图(面积无意义)
应用场景
适合的场景
-
当数据具有单个自变量时 当数据依赖于像客户年龄这样的单个变量时,应使用直方图。直方图可帮助查看者了解因变量的分布。例如,基于年龄的客户银行存款余额。
-
当数据具有连续范围时 当样本数据表示学生考试成绩等连续范围时,直方图很有用。当数据在其范围内存在显著差距时,直方图可能不适合。
-
当需要比较两个数据集时 直方图是比较两个数据集的频率分布的绝佳工具。例如,考虑不同年��龄组的顾客的购买次数。直方图可用于比较多个商店中的这些数据。
不适合的场景
-
当数据为非数字时 直方图最适用于具有连续数据范围的数值变量的图形表示。如果数据由性别或位置等非数字值组成,则直方图显然是不合适的。在这种情况下,可以使用饼图或条形图。
-
当样本数量较小时 抽取的样本数量过小,将会产生较大误差,可信度低,也就失去了统计的意义。因此,样本数不应少于 50 个。
-
当数据中存在较大间隙时 当样本数据连续时,直方图最适合。直方图表示属于不同条柱的数据点,因此当数据丢失或未定义时,图形效率低下。
案例
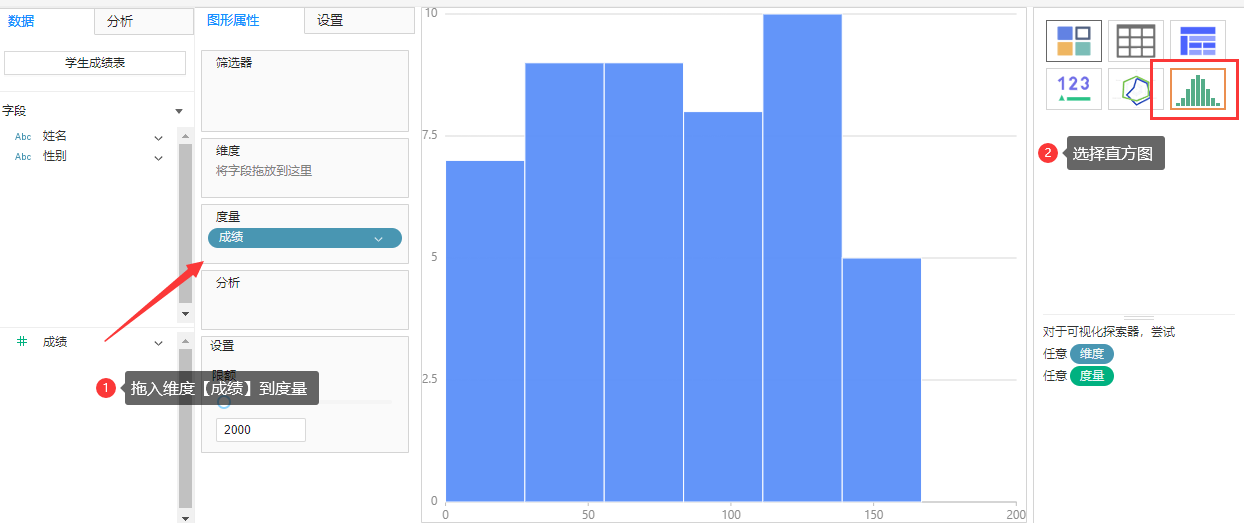
案例数据下载:学生成绩表
案例介绍:本案例是某班级60名学生的某项成绩表,满分150,作为该门课程的教师或校领导想要看学生的成绩分布,此时选用直方图进行展示比较合适。
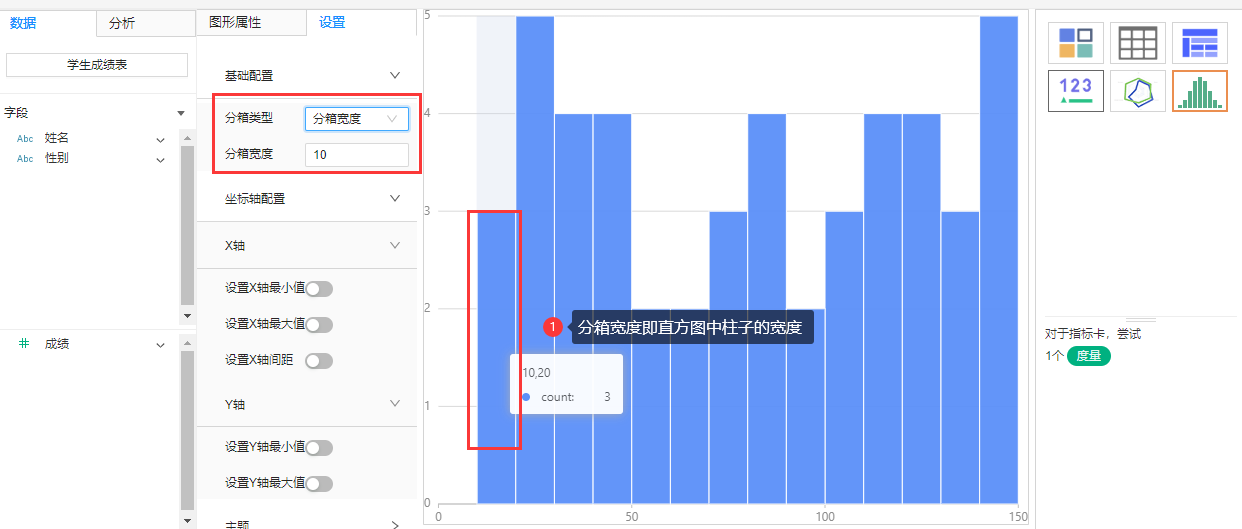
直方图制作流程: