Mean Shift
组件介绍
“Mean Shift” 控件基于核密度估计进行聚类操作。
Mean Shift(均值漂移)是基于密度的非参数聚类算法,其算法思想是假设不同簇类的数据集符合不同的概率密度分布,找到任一样本点密度增大的最快方向(最快方向的含义就是Mean Shift),样本密度高的区域对应于该分布的最大值,这些样本点最终会在局部密度最大值收敛,且收敛到相同局部最大值的点被认为是同一簇类的成员。
密度估计是指有给定样本集和求解随机变量的分布密度函数,解决这一问题的方法包括:参数估计和非参数估计。
参数估计:在我们已经知道观测数据符合某些模型的情况下,我们可以利用参数估计的方法来确定这些参数值,然后得出概率密度模型。前提是观测数据服从一个已知概率密度函数。
非参数估计:无需任何先验知识完全依靠特征空间中样本点计算其密度估计值.可以处理任意概率分布,不必假设服从已知分布;常用的无参数密度估计方法有:直方图法、最近邻域法和核密度估计法。MeanShift算法正属于核密度估计法。无需任何先验知识完全依靠特征空间中样本点计算其密度估计值。
- 输入:
- data:数据集
- 输出:
- data:处理后的数据集
- cen:每个簇的中心点
页面介绍
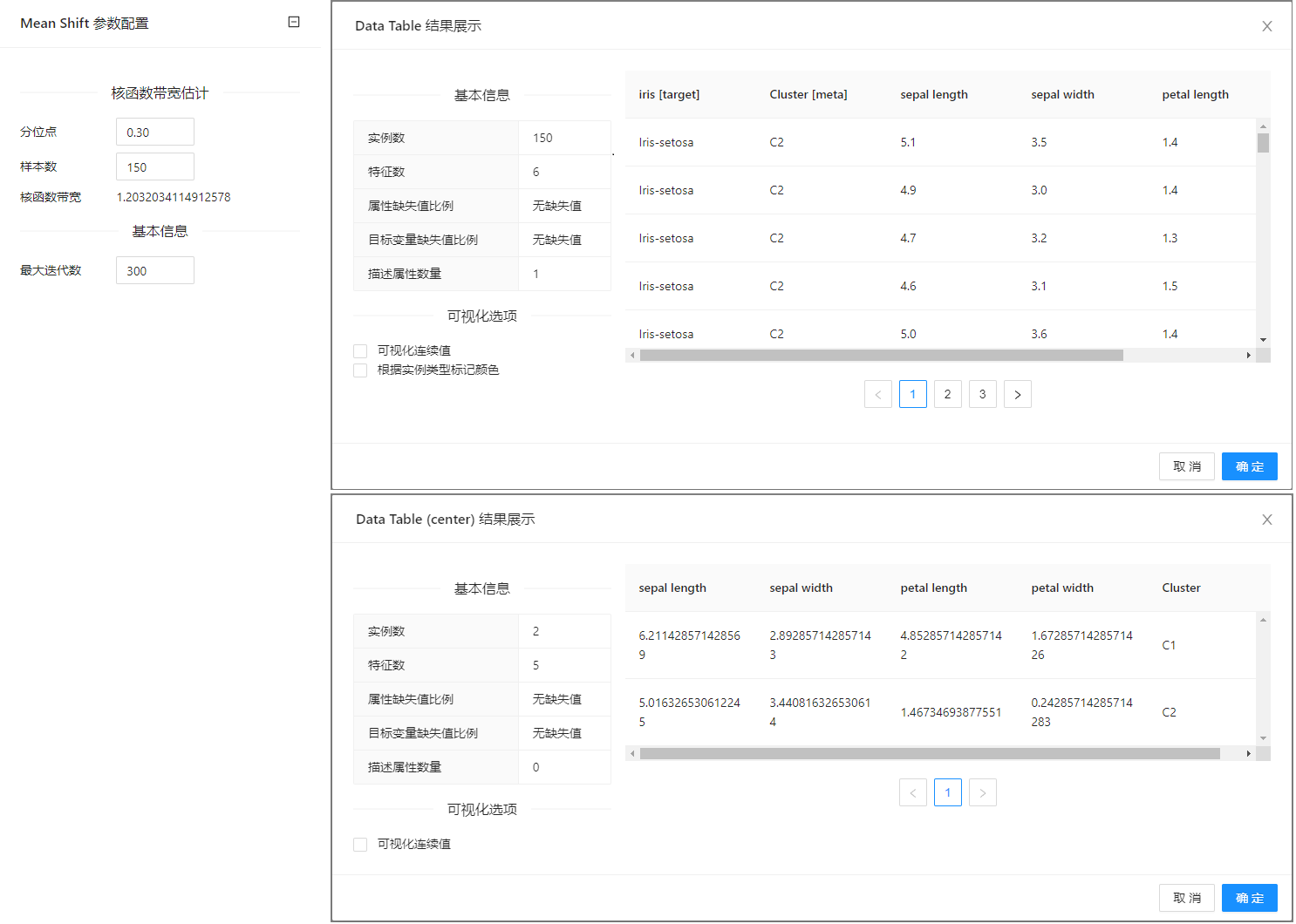
点击 “Mean Shift” 控件查看参数配置页面,如下图所示:
参数选项
| 选项 | 说明 | 取值范围 | 样例值 |
|---|---|---|---|
| 分位点 | 【0,1】之间 | 0~1 | 0.3 |
| 样本数 | 用于计算的实例数 | 1~10000 | 150 |
| 核函数宽带 | 根据参数计算出的核函数带宽 | ||
| 最大迭代数 | 算法运行的最大迭代次数 | 1~10000 | 300 |
使用案例
在下图所示的案例中,使用 “加载文件”(File) 控件加载数据集,连接 “Mean Shift” 控件进行聚类,之后连接 “查看数据”(Data Table) 控件查看聚类结果。
案例中加载 iris 数据集,案例中控件的配置以及执行结果如下图所示。